线段树基础
概念
线段树是一种基于分治思想的二叉树结构,用于在区间上进行信息统计,它能够平衡空间与时间复杂度,并且相较于树状数组,线段树是一种更加通用的结构
线段树由若干节点构成,每一个节点代表一个区间,线段树的根节点代表的区间是整个统计范围,叶子节点代表长度为1的元区间,即单个元素的值,对于每一个节点$[l,r]$,它的左子节点是$[l,mid]$,右子节点是$[mid+1,r]$,其中$mid=\lfloor \frac{l+r}{2} \rfloor$
由于线段树除了最后一层外是满二叉树,我们可以假设整棵线段树是一棵满二叉树,那么对于每一个节点$x$,它的左子节点编号为$2x$,右子节点编号为$2x+1$,在程序中,可以使用算术运算lc=2*x,rc=2*x+1;,也可以使用位运算lc=x<<1,rc=(x<<1)|1;
在最理想情况下,线段树为一棵满二叉树,所需的空间为$2N$,但是由于最后一层节点产生了空余,所以要将数组的长度开到$4N$才能保证不会越界
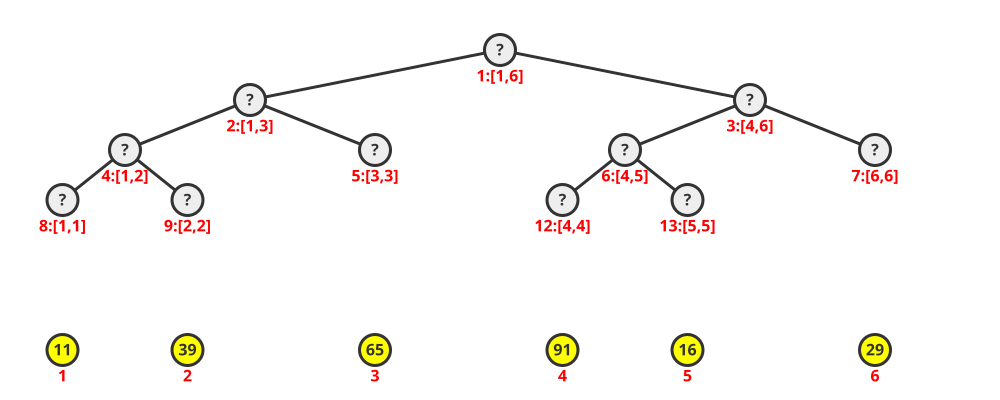
以下是线段树的可视化图:
建树
线段树采用递归建树,建树时可以将每个节点的范围记录在节点中(当然也可以不进行记录,每次递归时进行计算),记录区间的范围能够优化时间复杂度的常数
在建立完左右子树后,需要将当前节点的信息进行更新,为了使逻辑更清晰,同时方便应对将来要应对的复杂信息的更新,我们另定义一个内联函数push_up用于从左右子节点中获取数据更新父节点
线段树节点可以维护很多信息,这里以区间最大值为例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
struct node
{
int l,r;
long long dat;
}s[N<<2];
inline void push_up(int p)
{
s[p].dat=max(s[p<<1].dat,s[(p<<1)|1].dat);
}
void build(int p,int l,int r)
{
s[p].l=l,s[p].r=r;
if(l==r) {s[p].dat=a[l];return;}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build((p<<1)|1,mid+1,r);
push_up(p);
}
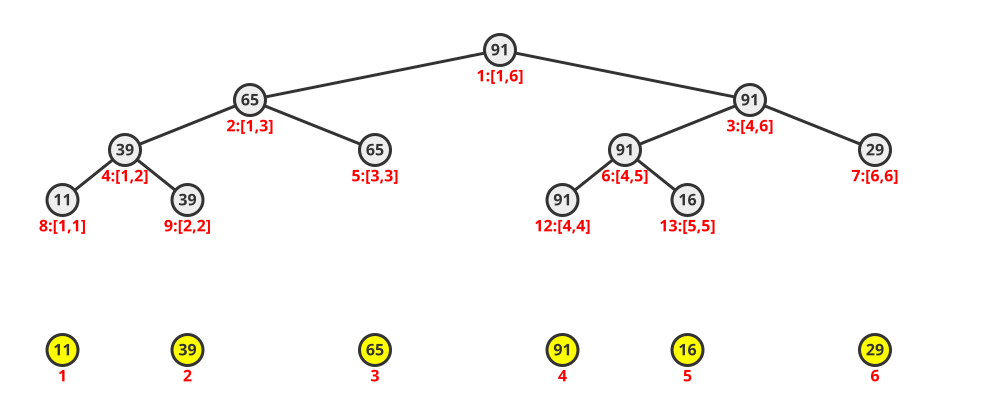
建立完成后,每个节点的信息都会被更新:
单点修改
单点修改是一条形如 “$C$ $x$ $v$” 的指令,表示把 $A[x]$ 的值修改为 $v$
我们从根节点出发,递归找到代表区间 $[x,x]$ 的叶子节点,然后从下往上更新 $[x,x]$ 以及它的所有祖先节点,时间复杂度为 $O(\log_2 N)$
代码如下,其中x和v是全局变量,不随递归而改变:
1
2
3
4
5
6
7
8
void change(int p)
{
if(s[p].l==s[p].r) {s[p].dat=v;return;}
int mid=(s[p].l+s[p].r)>>1;
if(x<=mid) change(p<<1);
else change((p<<1)|1);
push_up(p);
}
区间查询
区间查询是一条形如 “$Q$ $l$ $r$” 的指令,例如查询序列 $A$ 在区间 $[l,r]$ 上的最大值,即 $\max \limits_{l \le i \le r} A[i]$
我们需要从根节点开始,递归执行以下过程:
- 若 $[l,r] \subseteq [s[p].l,s[p].r]$ ,则立即回溯,并且该节点的 $dat$ 值为候选答案
- 若左子节点代表的范围与 $[l,r]$ 有重叠部分,那么递归访问左子节点
- 若右子节点代表的范围与 $[l,r]$ 有重叠部分,那么递归访问右子节点
1
2
3
4
5
6
7
8
9
long long query(int p)
{
if(l<=s[p].l&&r>=s[p].r) return s[p].dat;
int mid=(s[p].l+s[p].r)>>1;
long long res=-INF;
if(l<=mid) res=max(res,query(p<<1));
if(r>mid) res=max(res,query((p<<1)|1));
return res;
}
该查询过程会把询问区间 $[l,r]$ 在线段树上最多分成 $O(\log_2 N)$ 个节点,取它们最大值即可,所以时间复杂度也是 $O(\log_2 N)$
线段树进阶
接下来是线段树的进阶操作,将结合例题讲解
P3372 线段树 1
原题链接:https://www.luogu.com.cn/problem/P3372
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 $k$
- 求出某区间每一个数的和
输入格式
第一行包含两个整数 $n$, $m$ ,分别表示该数列数字的个数和操作的总个数。
第二行包含 $n$ 个用空格分隔的整数,其中第 $i$ 个数字表示数列第 $i$ 项的初始值。
接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数,表示一个操作,具体如下:
1 x y k:将区间 $[x, y]$ 内每个数加上 $k$。2 x y:输出区间 $[x, y]$ 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
输入输出样例
输入 #1
1
2
3
4
5
6
7
8
5 6
1 2 3 4 5
3 2 5
1 1 3 3
4 2 4
2 3 4 1
5 1 5
3 1 4
输出 #1
1
2
3
4
14
6
6
11
说明/提示
对于 $30\%$ 的数据:$n \le 8, m \le 10$ 对于 $70\%$ 的数据:$n \le {10}^3, m \le {10}^4$ 对于 $100\%$ 的数据:$1 \le n, m \le {10}^5$
延迟标记
之前讲过单点修改和区间查询都是 $O(\log_2 N)$ 的时间复杂度,但是如果仍然使用同样的方法进行区间修改复杂度会退化到 $O(N)$ ,这是不能接受的,可以发现,当在一次递归中产生 $[l,r] \subseteq [s[x].l,s[x].r]$ 的情况时,按照单点修改的操作流程,会将这个节点为根的整棵子树中的每一个节点进行信息的更新,如果在接下来的查询命令中这些信息没被用到,那么对没有访问到的节点进行修改是徒劳的
换言之,我们在递归到这一类节点时仍然可以像区间查询那样立即回溯,但是这个节点的所有子孙节点都还没被更新,所以我们要做一个延迟更新标记,标识:“该节点曾经被修改,但其子孙节点尚未更新”,当接下来的命令需要访问它的子节点时,再对子节点进行更新
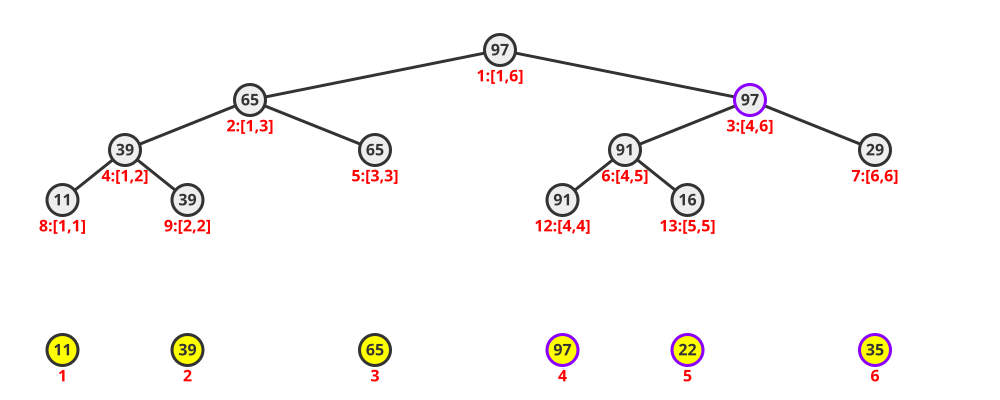
以上文所绘制的线段树为例,假如我们要对区间 $[4,6]$ 的每一个元素增加 $6$ ,由于 $3$ 号节点所代表的区间包含于我们的目标区间,我们可以在递归到 $3$ 号节点时为 $3$ 号节点打上 $+6$ 的增量延迟标记,如下图所示, $3$ 的所有子孙节点并没有进行更新操作:
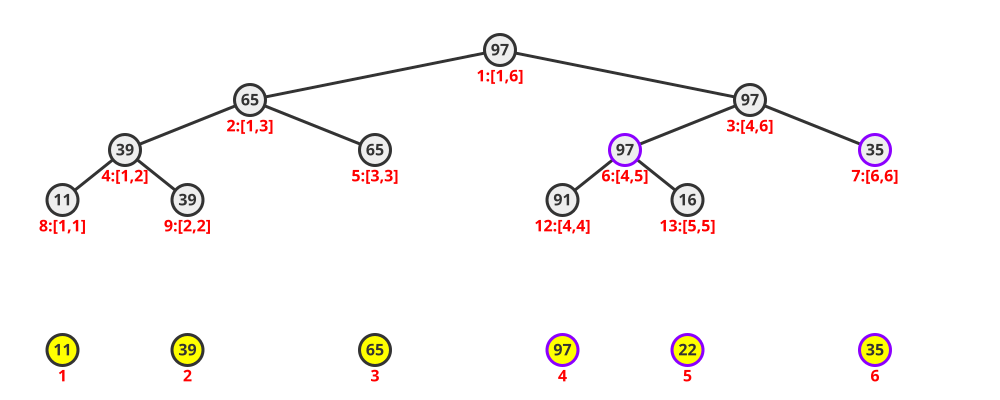
当接下来的指令需要访问 $3$ 的子节点时,将 $3$ 的左右子节点信息更新,并为它们打上增量延迟标记,同时将自己的增量延迟标记去除:
这样,每次进行区间修改时与区间查询的流程就相同了,时间复杂度为 $O(\log_2 N)$ ,而增量延迟标记下传每次的时间复杂度为 $O(1)$ ,不会影响总的时间复杂度
那么延迟标记具体该怎么实现呢?我们在原有的node结构体中添加一个变量add,该变量即为增量延迟标记,然后我们编写一个push_down内联函数用于在访问子节点之前对延迟标记进行下传更新
1
2
3
4
5
6
7
8
9
10
11
inline void push_down(int p)
{
if(s[p].add)
{
s[p<<1].sum+=s[p].add*(s[p<<1].r-s[p<<1].l+1);
s[(p<<1)|1].sum+=s[p].add*(s[(p<<1)|1].r-s[(p<<1)|1].l+1);
s[p<<1].add+=s[p].add;
s[(p<<1)|1].add+=s[p].add;
s[p].add=0;
}
}
这样每次区间修改时当递归到一个代表范围包含于目标范围的节点时就可以打上延迟标记立即回溯了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void add(int p)
{
if(s[p].l>=l&&s[p].r<=r)
{
s[p].sum+=k*(s[p].r-s[p].l+1);
s[p].add+=k;
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) add(p<<1);
if(r>mid) add((p<<1)|1);
push_up(p);
}
同样不要忘记在query函数中的相应位置也要加上push_down函数的调用
1
2
3
4
5
6
7
8
9
10
long long query(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].sum;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=0;
if(l<=mid) res+=query(p<<1);
if(r>mid) res+=query((p<<1)|1);
return res;
}
完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <cstdio>
using namespace std;
const int N=1e5+10,M=1e5+10;
struct node
{
int l,r;
long long sum,add;
}s[N<<2];
int n,m,op,l,r;
long long a[N],k;
inline long long read(){
register long long x=0,f=1;
register char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
inline void write(long long x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void push_up(int p)
{
s[p].sum=s[p<<1].sum+s[(p<<1)|1].sum;
}
inline void push_down(int p)
{
if(s[p].add)
{
s[p<<1].sum+=s[p].add*(s[p<<1].r-s[p<<1].l+1);
s[(p<<1)|1].sum+=s[p].add*(s[(p<<1)|1].r-s[(p<<1)|1].l+1);
s[p<<1].add+=s[p].add;
s[(p<<1)|1].add+=s[p].add;
s[p].add=0;
}
}
void build(int p,int l,int r)
{
s[p].l=l,s[p].r=r;
if(l==r)
{
s[p].sum=a[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build((p<<1)|1,mid+1,r);
push_up(p);
}
void add(int p)
{
if(s[p].l>=l&&s[p].r<=r)
{
s[p].sum+=k*(s[p].r-s[p].l+1);
s[p].add+=k;
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) add(p<<1);
if(r>mid) add((p<<1)|1);
push_up(p);
}
long long query(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].sum;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=0;
if(l<=mid) res+=query(p<<1);
if(r>mid) res+=query((p<<1)|1);
return res;
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++)
{
op=read();
if(op==1)
{
l=read(),r=read(),k=read();
add(1);
}
else
{
l=read(),r=read();
write(query(1));
putchar('\n');
}
}
return 0;
}
P3373 线段树 2
原题链接:https://www.luogu.com.cn/problem/P3373
题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 $x$
- 将某区间每一个数加上 $x$
- 求出某区间每一个数的和
输入格式
第一行包含三个整数 $n,m,p$,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 nn 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 mm 行每行包含若干个整数,表示一个操作,具体如下:
操作 $1$:格式:1 x y k 含义:将区间 $[x,y]$ 内每个数乘上 $k$
操作 $2$:格式:2 x y k 含义:将区间 $[x,y]$ 内每个数加上 $k$
操作 $3$:格式:3 x y 含义:输出区间 $[x,y]$ 内每个数的和对 $p$ 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 $3$ 的结果
输入输出样例
输入 #1
1
2
3
4
5
6
7
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出 #1
1
2
17
2
说明/提示
对于 $30\%$ 的数据:$n \le 8$ ,$m \le 10$ 对于 $70\%$ 的数据:$n \le 10^3$ ,$m \le 10^4$ 对于 $100\%$ 的数据:$n \le 10^5$ ,$m \le 10^5$
延迟标记的深度理解
延迟标记的本质,是对一个区间的延迟性操作,这个操作可以是加上一个数,乘上一个数,赋值等等,我们可以将其认为是进行一次函数的计算,用于延迟标记的操作必须要具有可积累性,也就是说无论多少次操作,我们都能通过一次操作来等效替代,比如加法就具备可积累性,例如一个元素被先后加上了若干个数,即为一次性加上这些数字之和,在这道题中,存在加法和乘法两种操作,现在我们就是要找到同时适用于这两种操作对应的函数
可以发现,我们设操作所对应的函数为 $f(x)$,不进行任何操作的情况下 $f(x)=x$,无论我们进行多少次加法和乘法操作,$x$ 的次数始终为 $1$,也就是说这一系列操作能用一个一次函数来等效替代,一次函数有两个参数,这里设为 $a$ 和 $b$,那么有:
\[f(x)=ax+b \\ f(x)+k=ax+b+k \\ kf(x)=k(ax+b)=akx+bk\]所以在每次进行加法操作时,只需 $b \gets b+k$,每次进行乘法操作时,$a \gets a \times k, b \gets b \times k$
最终我们只需要维护两个延迟标记,其余代码略作修改即可:
1
2
3
4
5
struct node
{
int l,r;
long long sum,a,b;
}s[N<<2];
本题要求输出取模后的答案,需要注意每次运算都要取模,防止溢出,下面是我的AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <cstdio>
using namespace std;
const int N=1e5+10,M=1e5+10;
struct node
{
int l,r;
long long sum,a,b;
}s[N<<2];
int n,m,op,l,r,mod;
long long k,a[N];
inline void push_up(int p)
{
s[p].sum=(s[p<<1].sum+s[(p<<1)|1].sum)%mod;
}
inline void push_down(int p)
{
if(s[p].a!=1||s[p].b!=0)
{
s[p<<1].sum=(s[p].a*s[p<<1].sum%mod+s[p].b*(s[p<<1].r-s[p<<1].l+1)%mod)%mod;
s[(p<<1)|1].sum=(s[p].a*s[(p<<1)|1].sum%mod+s[p].b*(s[(p<<1)|1].r-s[(p<<1)|1].l+1)%mod)%mod;
s[p<<1].a=(s[p<<1].a*s[p].a)%mod,s[p<<1].b=(s[p<<1].b*s[p].a%mod+s[p].b)%mod;
s[(p<<1)|1].a=(s[(p<<1)|1].a*s[p].a)%mod,s[(p<<1)|1].b=(s[(p<<1)|1].b*s[p].a%mod+s[p].b)%mod;
s[p].a=1,s[p].b=0;
}
}
void build(int p,int l,int r)
{
s[p].l=l,s[p].r=r,s[p].a=1;
if(l==r)
{
s[p].sum=a[l]%mod;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build((p<<1)|1,mid+1,r);
push_up(p);
}
void muti(int p)
{
if(s[p].l>=l&&s[p].r<=r)
{
s[p].sum=(s[p].sum*k)%mod;
s[p].a=(s[p].a*k)%mod,s[p].b=(s[p].b*k)%mod;
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) muti(p<<1);
if(r>mid) muti((p<<1)|1);
push_up(p);
}
void add(int p)
{
if(s[p].l>=l&&s[p].r<=r)
{
s[p].sum=(s[p].sum+k*(s[p].r-s[p].l+1))%mod;
s[p].b=(s[p].b+k)%mod;
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) add(p<<1);
if(r>mid) add((p<<1)|1);
push_up(p);
}
long long query(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].sum;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=0;
if(l<=mid) res+=query(p<<1);
if(r>mid) res+=query((p<<1)|1);
return res%mod;
}
int main()
{
scanf("%d%d%d",&n,&m,&mod);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&op,&l,&r);
if(op==3) printf("%lld\n",query(1));
else
{
scanf("%lld",&k),k%=mod;
if(op==1) muti(1);
else add(1);
}
}
return 0;
}
P6242 线段树 3
原题链接:https://www.luogu.com.cn/problem/P6242
题目详细信息
题目背景
本题是线段树维护区间最值操作与区间历史最值的模板
题目描述
给出一个长度为 $n$ 的数列 $A$,同时定义一个辅助数组 $B$,$B$ 开始与 $A$ 完全相同。接下来进行了 $m$ 次操作,操作有五种类型,按以下格式给出:
1 l r k:对于所有的 $i \in [l,r]$,将 $A_i$ 加上 $k$($k$ 可以为负数)2 l r v:对于所有的 $i \in [l,r]$,将 $A_i$ 变成 $\min(A_i,v)$3 l r:求 $\sum_{i=l}^{r}A_i$4 l r:对于所有的 $i \in [l,r]$,求 $A_i$ 的最大值5 l r:对于所有的 $i \in [l,r]$,求 $B_i$ 的最大值
在每一次操作后,我们都进行一次更新,让 $B_i \gets \max(B_i,A_i)$
输入格式
第一行包含两个正整数 $n,m$,分别表示数列 $A$ 的长度和操作次数。
第二行包含 $n$ 个整数 $A_1,A_2,\cdots,A_n$,表示数列 $A$。
接下来 $m$ 行,每行行首有一个整数 $op$,表示操作类型;接下来两个或三个整数表示操作参数,格式见【题目描述】。
输出格式
对于 $op \in {3,4,5}$ 的操作,输出一行包含一个整数,表示这个询问的答案
输入输出样例
输入 #1
1
2
3
4
5
6
7
8
5 6
1 2 3 4 5
3 2 5
1 1 3 3
4 2 4
2 3 4 1
5 1 5
3 1 4
输出 #1
1
2
3
4
14
6
6
11
说明/提示
样例说明 #1
| 操作次数 | 输入内容 | 操作 | 数列 | 输出结果 |
|---|---|---|---|---|
| 0 | $1,2,3,4,5$ | |||
| 1 | 3 2 5 |
求出 $[2,5]$ 所有数的和 | $1,2,3,4,5$ | 14 |
| 2 | 1 1 3 3 |
将 $[1,3]$ 内所有数加 $3$ | $4,5,6,4,5$ | |
| 3 | 4 2 4 |
求出 $[2,4]$ 所有数的最大值 | $4,5,6,4,5$ | 6 |
| 4 | 2 3 4 1 |
将 $[3,4]$ 所有数与 $1$ 取最小值 | $4,5,1,1,5$ | |
| 5 | 5 1 5 |
求出 $[1,5]$ 所有位置历史最大值的最大值 | $4,5,1,1,5$ | 6 |
| 6 | 3 1 4 |
求出 $[1,4]$ 所有数的和 | $4,5,1,1,5$ | 11 |
数据规模与约定
- 对于测试点 $1,2$,满足 $n,m\leq 5000$
- 对于测试点 $3,4$,满足 $op \in {1,2,3,4}$
- 对于测试点 $5,6$,满足 $op \in {1,3,4,5}$
- 对于全部测试数据,保证 $1\leq n,m\leq 5\times 10^5$,$-5\times10^8\leq A_i\leq 5\times10^8$,$op \in [1,5]$,$1 \leq l\leq r \leq n$,$-2000\leq k\leq 2000$,$-5\times10^8\leq v\leq 5\times10^8$
题目分析
这一题可以说是线段树的综合,涉及到的修改和查询操作很多,尤其是取 $\min$ 操作给我们带来了很大的麻烦,使得多个操作不能积累了,这时候我们就要维护更多的区间信息来辅助延迟标记,我们假设区间的最大值为 $max_a$,而区间的次大值为 $sec$,以及区间最大值的个数 $cnt$,进行 $\min$ 操作时:
- 当 $sec < v \le max_a$ 时,那么 $\min$ 操作只会让元素值为 $max_a$ 的元素变为 $v$,而其它元素不受影响,这样 $sum$ 减少的量即为 $cnt \times (max_a-v)$,$max_a$ 变为 $v$ 即可
- 当 $v>max_a$ 时,那么这个 $\min$ 操作对这个区间可以视为无效
- 当 $v \le sec$ 时,需要递归访问左右子节点
可以发现区间的最大值与非最大值有时是要区别对待的,因此我们要分别定义两个延迟增量标记 $add_a$ 和 $addmax_a$,分别表示非区间最大值的增量与区间最大值的增量,当进行加法操作时,两个增量均要被加上 $k$,而进行 $\min$ 操作时,只有 $addmax_a$ 会被加上 $v-max_a$
接着考虑区间历史最大值,与前面对应,我们需要变量 $max_b$ 存储区间历史最大值,$add_b$ 和 $addmax_b$ 分别表示非区间历史最大值增量和区间历史最大值增量
由于变量众多,我们另外定义一个函数 update用于将延迟增量标记加入到对应的节点中:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline void update(int p,long long add_a,long long add_b,long long addmax_a,long long addmax_b)
{
// node info
s[p].max_b=max(s[p].max_b,s[p].max_a+addmax_b);
s[p].sum+=add_a*(s[p].r-s[p].l+1-s[p].cnt)+addmax_a*s[p].cnt;
s[p].max_a+=addmax_a;
if(s[p].sec!=-INF) s[p].sec+=add_a;
// lazy tag
s[p].add_b=max(s[p].add_b,s[p].add_a+add_b);
s[p].addmax_b=max(s[p].addmax_b,s[p].addmax_a+addmax_b);
s[p].add_a+=add_a;
s[p].addmax_a+=addmax_a;
}
最主要是这三行比较难理解:
1
2
3
s[p].max_b=max(s[p].max_b,s[p].max_a+addmax_b);
s[p].add_b=max(s[p].add_b,s[p].add_a+add_b);
s[p].addmax_b=max(s[p].addmax_b,s[p].addmax_a+addmax_b);
第一行中的s[p].max_a+addmax_b表示当前的区间最大值加上历史最大值增量与原来的区间历史最大值取 $\max$
因为区间历史最大值这么更新,那么二、三行增量标记也相应更新
有了update函数,push_down函数就比较简洁了:
1
2
3
4
5
6
7
8
9
10
11
12
inline void push_down(int p)
{
// push down
int maxn=max(s[p<<1].max_a,s[(p<<1)|1].max_a);
if(s[p<<1].max_a==maxn) update(p<<1,s[p].add_a,s[p].add_b,s[p].addmax_a,s[p].addmax_b);
else update(p<<1,s[p].add_a,s[p].add_b,s[p].add_a,s[p].add_b);
if(s[(p<<1)|1].max_a==maxn) update((p<<1)|1,s[p].add_a,s[p].add_b,s[p].addmax_a,s[p].addmax_b);
else update((p<<1)|1,s[p].add_a,s[p].add_b,s[p].add_a,s[p].add_b);
// clear lazy tag
s[x].add_a=0,s[x].add_b=0,s[x].addmax_a=0,s[x].addmax_b=0;
}
在延迟标记下传的过程中,需要判断子节点代表区间的最大值是否是父节点代表区间的最大值,如果子结点中存在父节点的最大值,那么就把两个 $max$ 延迟标记下传,否则即使是子节点代表范围的最大值,也只会被传到非区间最大值的延迟增量标记,因为它并非是父节点代表范围的最大值
举个例子:假如某节点的 $max_a$ 为 $2$,而它的左子节点的 $max_a$ 为 $2$,右子节点的 $max_a$ 为 $1$,这时如果对该节点进行push_down,那么左子节点将传到 $add_a,add_b,addmax_a,addmax_b$,而右子节点将传到 $add_a,add_b,add_a,add_b$
push_up函数的实现比较简单,重点是如何计算 $cnt$:如果最大值仅出现在左子节点或右子节点中的一个,那么就将当前节点的 $cnt$ 赋值为该节点的 $cnt$,否则就将左右子节点的 $cnt$ 相加
1
2
3
4
5
6
7
8
9
10
11
inline void push_up(int p)
{
s[p].sum=s[p<<1].sum+s[(p<<1)|1].sum;
if(s[p<<1].max_a>s[(p<<1)|1].max_a)
s[p].max_a=s[p<<1].max_a,s[p].sec=max(s[p<<1].sec,s[(p<<1)|1].max_a),s[p].cnt=s[p<<1].cnt;
else if(s[p<<1].max_a<s[(p<<1)|1].max_a)
s[p].max_a=s[(p<<1)|1].max_a,s[p].sec=max(s[p<<1].max_a,s[(p<<1)|1].sec),s[p].cnt=s[(p<<1)|1].cnt;
else
s[p].max_a=s[p<<1].max_a,s[p].sec=max(s[p<<1].sec,s[(p<<1)|1].sec),s[p].cnt=s[p<<1].cnt+s[(p<<1)|1].cnt;
s[p].max_b=max(s[p<<1].max_b,s[(p<<1)|1].max_b);
}
最后给出AC代码(不要忘了使用快读快写)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
#include <cstdio>
#include <algorithm>
#define newline putchar('\n')
using namespace std;
const int N=5e5+10,M=5e5+10;
const long long INF=0x3f3f3f3f3f3f3f3f;
struct node
{
int l,r; // range
long long sum,max_a,max_b,cnt,sec; // node info
long long add_a,addmax_a,add_b,addmax_b; // lazy tag
}s[N<<2];
int n,m,op,l,r;
long long k,v,a[N];
inline long long read(){
register long long x=0,f=1;
register char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
inline void write(long long x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void update(int p,long long add_a,long long add_b,long long addmax_a,long long addmax_b)
{
// node info
s[p].max_b=max(s[p].max_b,s[p].max_a+addmax_b);
s[p].sum+=add_a*(s[p].r-s[p].l+1-s[p].cnt)+addmax_a*s[p].cnt;
s[p].max_a+=addmax_a;
if(s[p].sec!=-INF) s[p].sec+=add_a;
// lazy tag
s[p].add_b=max(s[p].add_b,s[p].add_a+add_b);
s[p].addmax_b=max(s[p].addmax_b,s[p].addmax_a+addmax_b);
s[p].add_a+=add_a;
s[p].addmax_a+=addmax_a;
}
inline void push_up(int p)
{
s[p].sum=s[p<<1].sum+s[(p<<1)|1].sum;
if(s[p<<1].max_a>s[(p<<1)|1].max_a)
s[p].max_a=s[p<<1].max_a,s[p].sec=max(s[p<<1].sec,s[(p<<1)|1].max_a),s[p].cnt=s[p<<1].cnt;
else if(s[p<<1].max_a<s[(p<<1)|1].max_a)
s[p].max_a=s[(p<<1)|1].max_a,s[p].sec=max(s[p<<1].max_a,s[(p<<1)|1].sec),s[p].cnt=s[(p<<1)|1].cnt;
else
s[p].max_a=s[p<<1].max_a,s[p].sec=max(s[p<<1].sec,s[(p<<1)|1].sec),s[p].cnt=s[p<<1].cnt+s[(p<<1)|1].cnt;
s[p].max_b=max(s[p<<1].max_b,s[(p<<1)|1].max_b);
}
inline void push_down(int p)
{
// push down
int maxn=max(s[p<<1].max_a,s[(p<<1)|1].max_a);
if(s[p<<1].max_a==maxn) update(p<<1,s[p].add_a,s[p].add_b,s[p].addmax_a,s[p].addmax_b);
else update(p<<1,s[p].add_a,s[p].add_b,s[p].add_a,s[p].add_b);
if(s[(p<<1)|1].max_a==maxn) update((p<<1)|1,s[p].add_a,s[p].add_b,s[p].addmax_a,s[p].addmax_b);
else update((p<<1)|1,s[p].add_a,s[p].add_b,s[p].add_a,s[p].add_b);
// clear lazy tag
s[p].add_a=0,s[p].add_b=0,s[p].addmax_a=0,s[p].addmax_b=0;
}
void build(int p,int l,int r)
{
s[p].l=l,s[p].r=r;
if(l==r)
{
s[p].sum=a[l],s[p].max_a=a[l],s[p].max_b=a[l],s[p].cnt=1,s[p].sec=-INF; // initial info
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build((p<<1)|1,mid+1,r);
push_up(p);
}
void add(int p)
{
if(s[p].l>=l&&s[p].r<=r)
{
update(p,k,k,k,k);
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) add(p<<1);
if(r>mid) add((p<<1)|1);
push_up(p);
}
void minimize(int p)
{
if(v>=s[p].max_a) return;
if(s[p].l>=l&&s[p].r<=r&&v>s[p].sec)
{
update(p,0,0,v-s[p].max_a,v-s[p].max_a);
return;
}
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
if(l<=mid) minimize(p<<1);
if(r>mid) minimize((p<<1)|1);
push_up(p);
}
long long query_sum(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].sum;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=0;
if(l<=mid) res+=query_sum(p<<1);
if(r>mid) res+=query_sum((p<<1)|1);
return res;
}
long long query_max_a(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].max_a;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=-INF;
if(l<=mid) res=max(res,query_max_a(p<<1));
if(r>mid) res=max(res,query_max_a((p<<1)|1));
return res;
}
long long query_max_b(int p)
{
if(s[p].l>=l&&s[p].r<=r) return s[p].max_b;
push_down(p);
int mid=(s[p].l+s[p].r)>>1;
long long res=-INF;
if(l<=mid) res=max(res,query_max_b(p<<1));
if(r>mid) res=max(res,query_max_b((p<<1)|1));
return res;
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
for(int i=1;i<=m;i++)
{
scanf("%d",&op);
switch (op)
{
case 1:
l=read(),r=read(),k=read();
add(1);
break;
case 2:
l=read(),r=read(),v=read();
minimize(1);
break;
case 3:
l=read(),r=read();
write(query_sum(1));
newline;
break;
case 4:
l=read(),r=read();
write(query_max_a(1));
newline;
break;
case 5:
l=read(),r=read();
write(query_max_b(1));
newline;
break;
}
}
return 0;
}