P2014选课（树形背包）

题目描述

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 $N$ 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程 $a$ 是课程 $b$ 的先修课即只有学完了课程 $a$，才能学习课程 $b$）。一个学生要从这些课程里选择 $M$ 门课程学习，问他能获得的最大学分是多少？

输入格式

第一行有两个整数 $N,M$ 用空格隔开。($1 \leq N \leq 300, 1 \leq M \leq 300$)

接下来的 $N$ 行,第 $I+1$ 行包含两个整数 $k_i$ 和 $s_i, k_i$ 表示第 $I$ 门课的直接先修课，$s_i$ 表示第 $I$ 门课的学分。若 $k_i=0$ 表示没有直接先修课（$1 \leq {k_i} \leq N, 1 \leq {s_i} \leq 20$）

输出格式

只有一行，选 $M$ 门课程的最大得分。

输入输出样例

输入 #1

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

输出 #1

13

分析

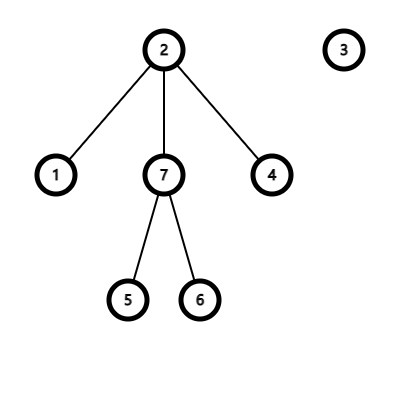
由于每一门课程的先修课只有 $0$ 或 $1$ 门，所以绘制出来将会是森林的结构：

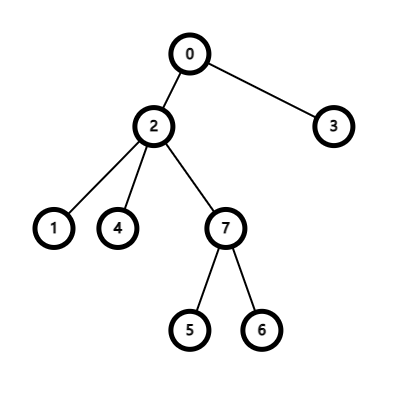
由于森林不方便处理，我们对其进行等效变换，由输入数据得到启发，可以将没有先修课的课程认为是先修课为 $0$ 的课程，这样要学任意课程，都必须先学课程 $0$，而课程 $0$ 是没有学分的（类似于开营仪式），并且我们要把之前能选 $m$ 门课程的条件改为能选 $m+1$ 门课程，这多出来的一门课程就是去学课程 $0$，这样森林中的所有树就合并成了一棵树：

可以在树上进行动态规划求解，我们用数组 $dp[i][j]$ 表示在以 $i$ 为根节点的子树中最多选择 $j$ 门课程所能达到的最大学分，那么朴素的状态转移方程为：

\[dp[i][j]=\max \{ \sum_{k=1}^{\left| son[i] \right|} dp[son[i][k]][x_k] | \sum_{k=1}^{\left| son[i] \right|}x_k=j, \forall x_k \ge 0 \}\]

通俗来讲就是根据节点的孩子数将 $j$ 门课程分成相应的份数从孩子节点的 $dp$ 上转移

这样相当于对一个自然数（可选课程数 $j$）进行有限个自然数的剖分，并且区分排列顺序，产生的情况数为 ${j + \lvert son[i] \rvert -1} \choose {\lvert son[i] \rvert}$ 种，所以最坏的情况下会有 ${n+m-1} \choose {m}$ 的数据规模，显然是不能接受的

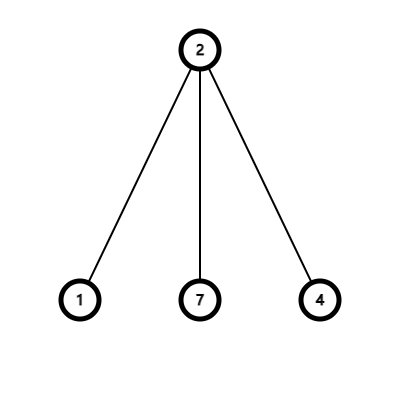
就以以下的父子结构为例：

我们将决策集合绘制成表格：

节点 $1$ 为根的子树	节点 $7$ 为根的子树	节点 $4$ 为根的子树
选 0 门课程	选 0 门课程	选 0 门课程
选 1 门课程	选 1 门课程	选 1 门课程
选 2 门课程	选 2 门课程	选 2 门课程
选 3 门课程	选 3 门课程	选 3 门课程
选 4 门课程	选 4 门课程	选 4 门课程
……	……	……

事实上，我们需要在每一列中选择一种方案，并且所有子树选的课程和要等于 $j$，这类似于一个分组01背包问题，表格中的每一列表示一组，每一种选择方案表示物品，而物品的“体积”就是选的课程数量，物品的价值就是相应的 $dp$ 的值

节点 1 为根的子树		节点 7 为根的子树		节点 4 为根的子树
体积	价值	体积	价值	体积	价值
0	dp[1][0]	0	dp[7][0]	0	dp[4][0]
1	dp[1][1]	1	dp[7][1]	1	dp[4][1]
2	dp[1][2]	2	dp[7][2]	2	dp[4][2]
3	dp[1][3]	3	dp[7][3]	3	dp[4][3]
4	dp[1][4]	4	dp[7][4]	4	dp[4][4]
……	……	……	……	……	……

最后总结一下，首先要进行树形dp，阶段是树上的每一个节点，状态是树上一个节点为根的子树能选择的课程数，决策是一个分组01背包

对于背包而言，阶段是目标节点的每一个孩子节点，状态是选择的物品（课程数），决策是分组01背包的状态转移方程，为了代码的简洁，我们将 $dp[i][j]$ 的意义更改为“在以 $i$ 为根节点的子树节点中（不包含该根节点）能选择的课程数为 $j$ 的情况下的最大学分

由于阶段是自叶子节点向根节点扩展，所以需要先 dfs 再 dp

代码部分

#include <cstdio>
#include <list>
using namespace std;

const int N=310,M=310;
int n,m,s[N],dp[N][M];
list<int> son[N];

void dfs(int x)
{
    if(son[x].empty()) return;
    for(list<int>::iterator it=son[x].begin();it!=son[x].end();it++)
    {
        dfs(*it);
        for(int i=m;i>=1;i--)
            for(int j=1;j<=i-1;j++)
                dp[x][i]=max(dp[x][i],dp[x][i-j]+dp[*it][j]+s[*it]);
    }
}

int main()
{
    scanf("%d%d",&n,&m),m++;
    for(int i=1;i<=n;i++)
    {
        int k;
        scanf("%d%d",&k,&s[i]);
        son[k].push_back(i);
    }
    dfs(0);
    printf("%d",dp[0][m]);
    return 0;
}